Estimation Methods: Inference Classical and Bayesian of Extended Inverse Exponential Distribution
DOI:
https://doi.org/10.62933/g25zz869Keywords:
Inverse Exponential, , MCMC, Bayesian estimator, general entropyAbstract
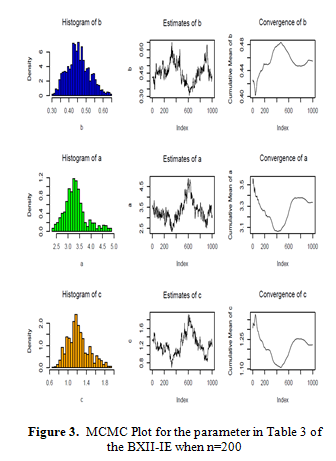
The parameters of the Burr XII-Inverse Exponential (BXII-IE) distribution were estimated in this work using a variety of Bayesian and non-Bayesian (Inference Classical) approaches. Methods like Maximum likelihood, least squares, weighted least squares, Maximum product space estimators, and Anderson Darling were developed for non-Bayesian estimators. Due to the lack of closed-form solutions for Bayesian estimates for certain loss functions squared error, general entropy, and linear-exponential and prior distributions for the parameters, Bayesian estimators had to be implemented. Bayesian estimation utilizing the Markov Chain Monte Carlo (MCMC) approach and seven non-Bayesian estimate techniques were tested for performance.
References
[1] Bashiru, S. O., Khalaf, A. A., Isa, A. M., & Kaigama, A. (2024). ON MODELING OF BIOMEDICAL DATA WITH EXPONENTIATED GOMPERTZ INVERSE RAYLEIGH DISTRIBUTION. Reliability: Theory & Applications, 19(3 (79)), 460-475.
[2] Bashiru, S. O., Khalaf, A. A., & Isa, A. M. (2024). TOPP-LEONE EXPONENTIATED GOMPERTZ INVERSE RAYLEIGH DISTRIBUTION: PROPERTIES AND APPLICATIONS. Reliability: Theory & Applications, 19(3 (79)), 59-77.
[3] Isa, A. M., Khalaf, A. A., & Bashiru, S. O. (2024). Some Properties of the Cosine Lomax Distribution with Applications.
[4] Isa, A. M., Bashiru, S. O., & Kaigama, A. (2024). Topp-Leone Exponentiated Burr XII Distribution: Theory and Application to Real-Life Data Sets. Iraqi Statisticians Journal, 1(1), 63-72.
[5] Khalaf, A. A., Ibrahim, M. Q., & Noori, N. A. (2024). [0, 1] Truncated Exponentiated Exponential Burr type X Distribution with Applications. Iraqi Journal of Science, 4428-4440.
[6] Noori, N. A., Khalaf, A. A., & Khaleel, M. A. (2024). A new expansion of the Inverse Weibull Distribution: Properties with Applications. Iraqi Statistians Journal, 1(1), 52-62.
[7] Khalaf, A., Yusur, K., & Khaleel, M. (2023). [0, 1] Truncated Exponentiated Exponential Inverse Weibull Distribution with Applications of Carbon Fiber and COVID-19 Data. Journal of Al-Rafidain University College For Sciences (Print ISSN: 1681-6870, Online ISSN: 2790-2293), (1), 387-399.
[8] Khalaf, A., & Khaleel, M. (2020). Truncated exponential marshall-olkin-gompertz distribution properties and applications. Tikrit Journal of Administration and Economics Sciences, 16, 483-497.
[9] Al-Habib, K. H., Khaleel, M. A., & Al-Mofleh, H. (2024). Statistical Propoerties and Application for [0, 1] Truncated Nadarajah-Haghighi Exponential Distribution. Ibn AL-Haitham Journal For Pure and Applied Sciences, 37(2), 376-392.
[10] Mahdi, G. A., Khaleel, M. A., Gemeay, A. M., Nagy, M., Mansi, A. H., Hossain, M. M., & Hussam, E. (2024). A new hybrid odd exponential-Φ family: Properties and applications. AIP Advances, 14(4).
[11] Khaleel, M. A., & Ahmed, D. D. (2024). The Gompertz Inverted Nadarajah-Haghighi (GoINH) Distribution Properties with Application to real data. Tikrit Journal of Administrative and Economic Sciences, 20(67 part 2).
[12] Latif, M. A. A., & Khaleel, M. A. (2023, December). The properties and application of a new extension exponentiated exponential distribution. In AIP Conference Proceedings (Vol. 2834, No. 1). AIP Publishing.
[13] Abbasi, J. N. A., Resen, I. A., Abdulwahab, A. M., Oguntunde, P. E., Al-Mofleh, H., & Khaleel, M. A. (2023, December). The right truncated Xgamma-G family of distributions: Statistical properties and applications. In AIP Conference Proceedings (Vol. 2834, No. 1). AIP Publishing.
[14] Yusur, K. A., & Khaleel, M. A. (2023, December). The new extension of Chen distribution using gompertz family properties and application. In AIP Conference Proceedings (Vol. 2834, No. 1). AIP Publishing.
[15] Khubbaz, A. F., & Khaleel, M. A. (2023, December). Properties of truncated inverse Weibull exponential distribution with application to lifetime data. In AIP Conference Proceedings (Vol. 2834, No. 1). AIP Publishing.
[16] Akarawak, E. E., Adeyeye, S. J., Khaleel, M. A., Adedotun, A. F., Ogunsanya, A. S., & Amalare, A. A. (2023). The inverted Gompertz-Fréchet distribution with applications. Scientific African, 21, e01769.
[17] Hammed, S. S., & Khaleel, M. A. (2023). Gompertz Topp–Leone invers Weibull Distributions: Some Properties and Application. Tikrit Journal of Administrative and Economic Sciences, 19(61 part 2).
[18] Khaleel, M. A., Ampered, A. I., & Nafal, A. K. (2023). Properties of [0, 1] Truncated Inverse Weibull Inverse Exponential distribution with Real Life Data Application. Tikrit Journal of Administrative and Economic Sciences, 19(Special Issue part 5).
[19] Madaki, U. Y., Bakar, M. R. A., Khaleel, M. A., & Handique, L. (2022). Kumaraswamy Burr Type X Distribution and Its Properties. ASEANA Science and Education Journal, 2(2), 11-38.
[20] Aidi, K., Seddik-Ameur, N., Ahmed, A., & Khaleel, M. A. (2022). The Topp-Leone Extended Exponential Distribution: Statistical properties, different estimation methods and applications to life time data. Pakistan Journal of Statistics and Operation Research, 817-836.
[21] Hashmi, S., Ahsan-ul-Haq, M., Zafar, J., & Khaleel, M. A. (2022). Unit Xgamma Distribution: Its Properties, Estimation and Application: Unit-Xgamma Distribution. Proceedings of the Pakistan Academy of Sciences: A. Physical and Computational Sciences, 59(1), 15-28.
[22] Eissa, F. Y., Sonar, C. D., Alamri, O. A., & Tolba, A. H. (2024). Statistical Inferences about Parameters of the Pseudo Lindley Distribution with Acceptance Sampling Plans. Axioms, 13(7): 443.
[23] Hamdy, A., & Almetwally, E. M. (2023). Bayesian and non-bayesian inference for the generalized power akshaya distribution with application in medical. Computational Journal of Mathematical and Statistical Sciences, 2(1): 31-51.
[24] Alsadat, N., Elgarhy, M., Tolba, A. H., Elwehidy, A. S., Ahmad, H., & Almetwally, E. M. (2023). Classical and Bayesian estimation for the extended odd Weibull power Lomax model with applications. AIP Advances, 13(9).
[25] Hasaballah, M. M., Balogun, O. S., & Bakr, M. E. (2024). Frequentist and Bayesian approach for the generalized logistic lifetime model with applications to air-conditioning system failure times under joint progressive censoring data. 9(10), 29346–29369.
[26] Irfan, M., & Sharma, A. K. (2024). Bayesian Estimation and Prediction for Inverse Power Maxwell Distribution with Applications to Tax Revenue and Health Care Data. Journal of Modern Applied Statistical Methods, 23(1), 1-29
[27] Khalaf, A. A. (2024). The New Strange Generalized Rayleigh Family: Characteristics and Applications to COVID-19 Data. Iraqi Journal For Computer Science and Mathematics, 5(3), 32.
[28] Hammed, S., & Khaleel, M. (2023). Some Properties and Applications of the Gompertz Topp-Leone Inverse Exponential Distribution. Journal of Al-Rafidain University College For Sciences (Print ISSN: 1681-6870, Online ISSN: 2790-2293), (1), 374-386.
[29] Al-Noor, N. H., Khaleel, M. A., & Assi, N. K. (2022). The Rayleigh Gompertz distribution: Theory and real applications. International Journal of Nonlinear Analysis and Applications, 13(1), 3505-3516.
[30] Abdullah, Z. M., Hussain, N. K., Fawzi, F. A., Abdal-Hammed, M. K., & Khaleel, M. A. (2022). Estimating parameters of Marshall Olkin Topp Leon exponential distribution via grey wolf optimization and conjugate gradient with application. International Journal of Nonlinear Analysis and Applications, 13(1), 3491-3503.
[31] Khaleel, M. A., Abdulwahab, A. M., Gaftan, A. M., & Abdal-hammed, M. K. (2022). A new [0, 1] truncated inverse Weibull rayleigh distribution properties with application to COVID-19. International Journal of Nonlinear Analysis and Applications, 13(1), 2933-2946.
[32] Khalaf, A. A. (2022, November). [0, 1] Truncated exponentiated exponential gompertz distribution: Properties and applications. In AIP Conference Proceedings (Vol. 2394, No. 1). AIP Publishing.
[33] Swain J., Sekhar V., and James R. W. (1988). Least-squares estimation of distribution functions in Johnson’s translation system. Journal of Statistical Computation and Simulation, 29(4), 271–297.
[34] Habib, K. H., Khaleel, M. A., Al-Mofleh, H., Oguntunde, P. E., & Adeyeye, S. J. (2024). Parameters Estimation for the [0, 1] Truncated Nadarajah Haghighi Rayleigh Distribution. Scientific African, 23, e02105.
[35] Kao J. H. K., Computer Methods for Estimating Weibull Parameters in Reliability Studies, IRE Transactionson Reliability and Quality Control, vol. PGRQC-13, 15-33.
[36] Kao J. H.K. (1958). Computer methods for estimating Topp Leone parameters in reliability studies. IRE Transactions on Reliability and Quality Control, 1958, 15–22.
[37] Anderson T. W., & Darling D. A. (1952). Asymptotic theory of certain goodness of fit criteria based on stochastic processes. The annals of mathematical statistics, 193–212
[38] Chopin, N. (2009). Jim Albert: Bayesian computation with R: Springer, 2007. ISBN: 978-0-387-71384-7.
[39] Mood, A. M. (1950). Introduction to the Theory of Statistics.
[40] Kim, S., Lee, J. Y., & Sung, D. K. (2003). A shifted gamma distribution model for long-range dependent internet traffic. IEEE Communications Letters, 7(3), 124-126.
[41] Varian, H.R. (1975). A Bayesian approach to real estate assessment. In Studies in Bayesian econometric and statistics in Honor of Leonard J. Savage;Wiley Online Library: Hoboken, NJ, USA, 195–208.
[42] Almetwally, E. M., Alharbi, R., Alnagar, D., & Hafez, E. H. (2021). A new inverted topp-leone distribution: applications to the COVID-19 mortality rate in two different countries. Axioms, 10(1), 25.
[43] Khalaf, A. A. (2024). The New Strange Generalized Rayleigh Family: Characteristics and Applications to COVID-19 Data. Iraqi Journal For Computer Science and Mathematics, 5(3), 32.
[44] Khalaf, A., Yusur, K., & Khaleel, M. (2023). [0, 1] Truncated Exponentiated Exponential Inverse Weibull Distribution with Applications of Carbon Fiber and COVID-19 Data. Journal of Al-Rafidain University College For Sciences (Print ISSN: 1681-6870, Online ISSN: 2790-2293), (1), 387-399.
[45] Shah, Z., Khan, D. M., Khan, I., Ahmad, B., Jeridi, M., & Al-Marzouki, S. (2024). A novel flexible exponent power-X family of distributions with applications to COVID-19 mortality rate in Mexico and Canada. Scientific Reports, 14(1), 8992.
Downloads
Published
Issue
Section
License
Copyright (c) 2025 Alaa A. Khalaf, Mundher A. khaleel (Author)

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Licensed under a CC-BY license: https://creativecommons.org/licenses/by-nc-sa/4.0/







