Bathtub Curve in Reliability Analysis. A Review
DOI:
https://doi.org/10.62933/nfdxjj93Abstract
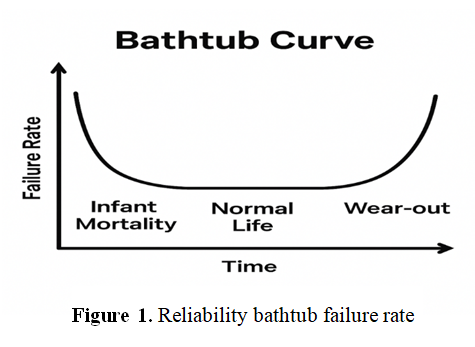
The bathtub curve is a popular concept and an important tool in reliability analysis. It describes the pattern or shape of the hazard rate function of products or systems throughout their life cycles over time. It helps in understanding failure modes and identifying critical periods in the systems life cycle in many fields such as engineering, quality management, electronics manufacturing, and other applied fields. This paper reviews the stages of the curve in some detail, along with everything that has been written by researchers on statistical estimation methods for the failure rate at each stage, highlighting the distributions related to this curve. It also addresses how to identify the points of change and transformation in this curve and the extent of its impact on preventive maintenance. The paper concludes with some critical points and objections to the bathtub curve.
References
1-Ammar M. Sarhan.(2017). A two-parameter discrete distribution with bathtub hazard shape. Communications for statistical applications methods, vol.24,no.1,pp.15-27.
2-Ammar M. Sarhan .(2019). Bayesian analysis of the discrete two-parameter bathtub hazard distribution. Journal of mathematical sciences and modeling , ,2(3), pp. 183-192.
3- Ammar M. Sarhan and Mazen Zaindin.(2009). Modified Weibull distribution. Applied Sciences, Vol.11, pp. 123-136.
4-Bell System Technical Journal(1976).Bell Telephone Laboratories 55(5),789-791.
5-C.D.Lai,Min Xie,D.N.P.Murthy.(2003) A modified weibull distribution.IEEE Transaction on reliability, vol.52,no.1.
6-Dennis J.Wilkins.The bathtub curve and product failure behavior.Reliability hot wire,2002,issue 21.
7- E. HAUPT ,H. SChabE .(1992). A New Model for a Lifetime Distribution with Bathtub Shaped Failure Rate .Mtcroelectron. Reliability. Vol. 32, No. 5, pp. 633-639.
8- Elvira Haupt, Hendrik Schaibe.(1997). The TTT transformation and a new bathtub distribution model. Journal of Statistical Planning and Inference, vol. 60, pp. 229- 240.
9-F.K.Wang.(2000). Anew model with bathtub shaped failure rate using an additive Burr XII distribution. Reliability Engineering & System Safety.vol.70.pp.305-312
10-Glaser, R.E. (1980). Bathtub and related failure rate characterizations, J. Amer. Statist. Assoc. 75,pp. 667 672.
11- Govind S. Mudholka, De0 Kumar Srivastava.(1993). Exponentiated Weibull Family for Analyzing Bathtub Failure-Rate Data. IEEE TRANSACTIONS ON RELIABILITY, VOL. 42, NO. 2.pp.299-302
12-Georgia-Ann Klutke, Peter C. Kiessler, and M. A. Wortman.(2003). ACritical Look at the Bathtub Curve. IEEE TRANSACTIONS ON RELIABILITY, VOL. 52, NO. 1.
13-Hjorth,U.(1980).Reliability distribution with increasing ,decreasing ,constant and bathtub shaped failure rate.Technometrics. 22(1)pp.99-107
14-Harish Kumar N.S.,R.P.Choudhary,Ch.S.N.Murthy.(2018).Failure rate and reliability of the KOMATSU hydraulic excavator in surface limestone mine.AIP conference proceedingsvol.1943,issue 1.
15-Jamal N.Al Abbasi, Mundher A. Khleel,Moudher Kh. Abdel-hameed.(2019). A uniform distribution with bathtub – shaped failure rate with simulation and application. Mathematical sciences. vol.13,pp.105-114.
16-K.S. Wang,F.S.Hsu . P.P.Liu.(2002). Modeling the bathtub shape hazard rate function in terms of reliability . Reliability Engineering & System Safety. 75 pp.397-406.
17-Kuocheng Chou&Kwei Tang.(1992). Burn-in Time and Estimation of Change-Point with Weibull-Exponential Mixture Distribution. Decision Sciences. vol.23.Issue 4.pp.973-990.
18- L. C. Méndez-González et al .(2022) The additive Perks distribution and its applications in reliability analysis. Quality Technology & Quantitative Management . https://doi.org/10.1080/16843703.2022.2148884
19-LAILA A. AL-ESSA et al.(2023). A NEW FLEXIBLE FOUR PARAMETERS BATHTUB CURVE failure rate model,and its application to right censord.IEEE ACCESS.vol.11,PP.50130-50144.
20- L. C. Méndez-González et al.(2023).The Chen–Perks Distribution: Properties and Reliability Applications , Mathematics . 11, 3001. https://doi.org/10.3390/math11133001.
21-M. SHAFIQ AND R. VIERTL.(2017). Bathtub Hazard Rate Distributions and Fuzzy Life Times, Iranian Journal of Fuzzy Systems Vol. 14, No. 5, pp. 31-41.
22- Mi.J. (1995).Bathtub failure rate and upside-down bathtub mean residual life,IEEE Transactions on Reliability . vol.44 Issu.3.
23--Mohammad Nadjafi , Mohammad Ali Farsi.(2021). Reliability analysis of system with timing function and dependency using fuzzy –bathtub failure rates.International journal of system assurance engineering and management.vol 12,pp.919-930.
24-Mohammad Nadjafi , Mohammad Ali Farsi.(2018). Fault trees analysis using expert opinion based on Fuzzy bathtub failure rates.Quality and reliability engineering international .vol.34, no.3.
25- M. H. TAHIR, GAUSS M. CORDEIRO, AYMAN ALZAATREH, M. MANSOOR4 AND M. ZUBAIR.(2016). A New Weibull-Pareto Distribution: Properties and Applications. Communication in Statistics- Simulation and Computation. VOL.45,issue 10.
26- MURARI MITRA ,SUJIT K. BASU .(1995). CHANGE POINT ESTIMATION IN NON-MONOTONIC AGING MODELS. Ann. Inst. Statist. Math. Vol. 47, No. 3,pp. 483-491 .
27-Mustapha Muhammad et al.(2024). A new three parameter bathtub and increasing failure rate model with application to real data. Pakistan journal of statistics and operation research. vol.20 no.1,pp.49-67.
28-Mark Bebbington,Chin Diew,Ricardas Zitikis.(2008).Estimation the turning point of a bathtub –shaped failure distribution.Journal of statistical planning ans inference.vol.138,issue 4,pp.1157-1166.
29- Makram Krit, Abdelwaheb Rebaa. Modeling of the effect of corrective and preventive maintenance with bathtub failure intensity.(2013).International journal of technology.vol.2 ,pp.157-166.
30-Makram Krit, Abdelwaheb Rebaa.(2011). An estimate of maintence efficiency in Brown-Proschen imperfect repair model with bathtub failure intensity. Journal of Industrial Engineering and Management.3(1) , pp.88-101
31-M.Xie , C.D. Lai. Reliability analysis using an additive Weibull model with bathtub-shaped failure rate function. Reliability Engineering & System Safety ,1995,52.pp.87-93.
32-Manuel S. Alvarez-Alvarado1 , Dilan Jayaweera.(2018).Bathtub curve as a markovian process to describe the reliability of repairable components. IET Generation Transmission& Distribution, Vol. 12 Iss. 21, pp. 5683-5689.
33-Magne Vollen Aarset.(1987).How to Identify a Bathtub Hazard Rate, IEEE TRANSACTIONS ON RELIABILITY, VOL. R-36, NO. 1.
34-M.Xie &C.D.Lai.(1996).Reliability analysis using additive Weibull model with bathtub – shaped failure rate function. Reliability Engineering and System Safety, 52. 87-93.
35-M. Xie, , T.N. Goh, Y. Tang.(2004). On changing points of mean residual life and failure rate function for some generalized Weibull distributions. Reliability Engineering and System Safety.vol 84,pp. 293–299.
36-M.Xie,T.N.Goh ,P.Ranjan.(2002).Some effective control chart procedures for reliability monitoring. Reliability Engineering & System Safety.vol.77,pp.143-150.
37- R.Jiang.(2013).Two methods to estimate the change points of a bathtub curve.,International journal of performability engineering,vol.9,no.5,pp.569-579.
38-R.Jiang.(2013). Determination of Two Change Points of a Bathtub Failure Rate Curve, ,19th international conference on industrial engineering and engineering management ,pp.619-629. 10.1007/978-3-642-38433-2_67
39-Ronald W. Smith,Duane L. Dietrch.(1994).The bathtub curve:An alternative explanation.proceedings Annual reliability and maintainability symposium.
40- Robab Aghazadeh Chakherlou,Mohammad Pourgol,Kamran Sepanloo.(2017). Change points estimations of bathtub-shaped hazard functions.International Journal of systems assurance engineering and management.vol.8,no.3,pp.553-559.
41-Suleman Nasiru, Albert Luguterah. (2015).The new weibull-pareto distribution. Pakistan journal of statistics and operation research.vol.XI,NO.1,PP.103-114.
42-Tan Cheng .(2006). A critical discussion on bath-tub curve. 42 annual conference of the Chinese society for quality and the 12th national quality management symposium.
43-Xuesiao Du .et al.Reliability analysis of repairable systems based on two-segment bathtub shaped failure intensity function.IEEE ACCESS ,2018,vol.6,pp.52374-52384.
44- Wikipedia contributors .(2025, March) Bathtub Curve. In Wikipedia , the Free Encyclopedia https://en.wikipedia.org/wiki/Bathtub_curve
45-Vigneshwar.(2025,July 21).What is a bathtub curve? How to measure asset reliability. Facilio. https://facilio.com/learn/what-is-bathtub-curve/
46-Xiaohong Wang, ChuangYu, and YuxiangLi.(2015). A New Finite Interval Lifetime Distribution Model for Fitting Bathtub-Shaped Failure Rate Curve, Mathematical Problems in Engineering Volume, Article ID 954327, 6 pages.
47-Yann Dijoux.(2009). An virtual age model based on a bathtub shaped intial intensity. Reliability Engineering & System Safety .vol.94,issue 5.pp.982-989
46- Wikipedia contributors .(2025, October ) Bathtub Curve. In Wikipedia , the Free Encyclopedia https://en.wikipedia.org/wiki/Bathtub_curve
47-Vigneshwar.(2025,July 21).What is a bathtub curve? How to measure asset reliability. Facilio. https://facilio.com/learn/what-is-bathtub-curve/
Downloads
Published
Issue
Section
License
Copyright (c) 2025 Suhad Ahmed Abdullah , Rabab Abdulrida Saleh (Author)

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Licensed under a CC-BY license: https://creativecommons.org/licenses/by-nc-sa/4.0/







