Data Modelling and Analysis Using Odd Lomax Generalized Exponential Distribution: an Empirical Study and Simulation
DOI:
https://doi.org/10.62933/dv0vyb66Keywords:
HOLGE distribution, LSE_s method, Quantile function, Incomplete Moments, Renyi entropy, Order statisticsAbstract
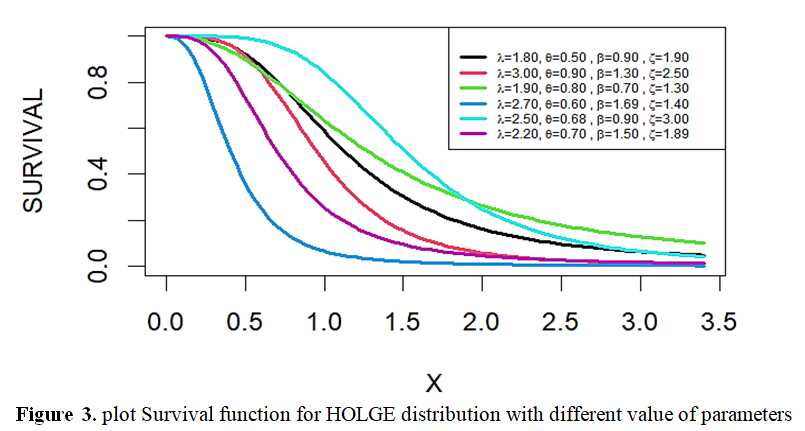
This study is based on the formulation of a new probabilistic model called the generalized singular Lomax exponential distribution using the singular Lomax generator and the exponential distribution. The proposed distribution is very flexible in modelling age data with both decreasing and increasing (non-monotonic) shapes. We define the probability density function (pdf) and cumulative distribution function (CDF) for the proposed distribution. Some mathematical properties of the proposed distribution such as the quantum function and moments are derived and for the incomplete moments the Renyi entropy of the proposed distribution is also obtained. Furthermore, the paper discusses model parameters in three different techniques, with Monte Carlo simulations to determine the efficiency of estimating the HOLGE distribution, with a comparison with three benchmarks to determine the best estimation method. A practical application is also carried out on two types of data that include the survival times of 72 guinea pigs infected with virulent tuberculosis bacilli, where the efficiency of the HOLGE distribution analysis is determined by comparing it to six other distributions using 4 information criteria and 4 statistical measures, which demonstrated the efficiency and flexibility of the HOLGE distribution.
References
[1] A. A. Al-Babtain, M. K. Shakhatreh, M. Nassar and A. Z. Afify, "A new modified Kies family: Properties, estimation under complete and type-II censored samples," Mathematics and engineering applications, p. 1345, 8 8 2020.
[2] L. Handique, M. A. ul Haq and C. Subrata, "Generalized Modified exponential-G family of distributions: its properties and applications," International Journal of Mathematics and Statistics, pp. 1-17, 1 21 2020.
[3] M. Aslam, Z. Asghar, Z. Hussain and S. F. Shahc, "A modified TX family of distributions: classical and Bayesian analysis," Journal of Taibah University for Science, pp. 254-264, 1 14 2020.
[4] M. A. Khaleel, P. E. Oguntunde, J. N. Al Abbasi, N. A. Ibrahim and M. H. AbuJarad, "The Marshall-Olkin Topp Leone-G family of distributions: A family for generalizing probability models," Scientific African, p. e00470, 8 2020.
[5] Y. Wang, Z. Feng and A. Zahra, "A new logarithmic family of distributions: Properties and applications," CMC-Comput. Mater. Contin, p. 919–929, 66 2021.
[6] A. S. Hassan, A. I. Al-Omari, R. R. Hassan and G. A. Alomani , "The odd inverted Topp Leone–H family of distributions: Estimation and applications," Journal of Radiation Research and Applied Sciences, pp. 365-379, 3 15 2022.
[7] J. T. Eghwerido, F. I. Agu and O. J. Ibidoja, "The shifted exponential-G family of distributions: Properties and applications," Journal of Statistics and Management Systems, pp. 43-75, 1 25 2022.
[8] A. B. Odeyale, S. U. Gulumbe, U. Umar and K. O. Aremu, "New Odd Generalized Exponentiated Exponential-G Family of Distributions," UMYU Scientifica, pp. 56-64, 4 2 2023.
[9] S. Hussain, M. U. Hassan, M. S. Rashid and R. Ahmed, "Families of Extended Exponentiated Generalized Distributions and Applications of Medical Data Using Burr III Extended Exponentiated Weibull Distribution," Mathematics, p. 3090, 14 11 2023.
[10] A. I. Ishaq, U. Panitanarak, A. A. Alfred , A. A. Suleiman and H. Daud, "The Generalized Odd Maxwell-Kumaraswamy Distribution: Its Properties and Applications," Contemporary Mathematics, pp. 711-742, 2024.
[11] N. A. Noori, A. A. Khalaf and M. A. Khaleel, "A New Generalized Family of Odd Lomax-G Distributions Properties and Applications," Advances in the Theory of Nonlinear Analysis and Its Application, pp. 1-16, 4 7 2023.
[12] A. A. Khalaf, M. Q. Ibrahim and N. A. Noori, "[0,1]Truncated Exponentiated Exponential Burr type X Distributionwith Applications," Iraqi Journal of Science, pp. 4428-4440, 8 65 2024.
[13] N. A. Noori, "Exploring the Properties, Simulation, and Applications of the Odd Burr XII Gompertz Distribution," Advances in the Theory of Nonlinear Analysis and Its Application, pp. 60-75, 4 7 2023.
[14] N. A. Noori and M. A. khaleel, "Estimation and Some Statistical Properties of the hybrid Weibull Inverse Burr Type X Distribution with Application to Cancer Patient Data," Iraqi Statisticians Journal, pp. 8-29, 2 1 2024.
[15] N. A. Noori, A. A. Khalaf and M. A. Khaleel, "A new expansion of the Inverse Weibull Distribution: Properties with Applications," Iraqi Statistians Journal, pp. 52-62, 1 1 2024.
[16] A. F. Khubaz, M. K. Abdal-Hameed, N. H. Mohamood and M. A. Khaleel, "Gompertz Inverse Weibull Distribution, some statistical properties with Application Real Dataset," Tikrit Journal of Administration and Economics Sciences, 19 2023.
[17] A.-E. A. M. Teamah, A. A. Elbanna and A. M. Gemeay, “FRÉCHET-WEIBULL DISTRIBUTION WITH APPLICATIONS TO EARTHQUAKES DATA SETS,” Pakistan Journal of Statistics, vol. 36, no. 2, pp. 135-147, 2020.
[18] H. Klakattawi, D. Alsulami, M. Abd Elaal, S. Dey and L. Baharith, "A new generalized family of distributions based on combining Marshal-Olkin transformation with TX family," PloS one, p. e0263673, 2 17 2022.
[19] A. A. Khalaf and M. khaleel, "The New Strange Generalized Rayleigh Family: Characteristics and Applications to COVID-19 Data," Iraqi Journal For Computer Science and Mathematics, vol. 5, no. 3, pp. 92-107, 2024.
[20] A. L. Solomon Sarpong and S. Nasiru, "Odd Chen-G family of distributions," Annals of Data Science, pp. 369-391, 2 9 2022.
[21] B. Muhammad, M. MOHSIN and M. ASLAM, "Weibull-exponential distribution and its application in monitoring industrial process," Mathematical Problems in Engineering, pp. 1-13, 2021.
[22] E. E. Akarawak, S. J. Adeyeye, M. A. Khaleel, A. F. Adedotun, A. S. Ogunsanya and A. A. Amalare, "the inverted Gompertz-Fréchet distribution with applications," Scientific African, p. e01769, 2023.
[23] J. N. Al Abbasi, I. A. Resen, A. M. Abdulwahab, P. E. Oguntunde, H. Al-Mofleh and M. A. Khaleel, "The right truncated Xgamma-G family of distributions: Statistical properties and applications," AIP Conference Proceedings, 1 2834 2023.
[24] K. H. Habib, A. M. Salih, M. A. Khaleel and M. K. Abdal-hammed, "OJCA Rayleigh distribution, Statistical Properties with Application," Tikrit Journal of Administration and Economics Sciences, 19 2023.
[25] P. E. Oguntunde, M. A. Khaleel, H. I. Okagbue and O. A. Odetunmibi, " the Topp–Leone Lomax (TLLo) distribution with applications to airbone communication transceiver dataset," Wireless Personal Communications, pp. 349-360, 2019.
[26] H. M. Almongy, E. M. Almetwally, H. M. Aljohani, A. S. Alghamdi and E. H. Hafez, "A new extended Rayleigh distribution with applications of COVID-19 data," Results in Physics, p. 104012, 23 2021.
[27] K. H. Al-Habib, M. A. Khaleel and H. Al-Mofleh, "A new family of truncated nadarajah-haghighi-g properties with real data applications," Tikrit Journal of Administrative and Economic Sciences, p. 2, 61 19 2023.
[28] F. Chipepa, B. O. Oluyede and B. Makubate, "A New Generalized Family of Odd Lindley-G Distributions With Application," International Journal of Statistics and Probability, pp. 1-23, 6 8 2019.
[29] K. H. Habib , M. A. Khaleel, H. Al-Mofleh, P. E. Oguntunde and S. J. Adeyeye, "Parameters Estimation for the [0, 1] Truncated Nadarajah Haghighi Rayleigh Distribution," Scientific African, p. e02105, 2024.
[30] J. Farrukh, M. A. Nasir, M. H. Tahir and N. H. Montazeri, "The odd Burr-III family of distributions," Journal of Statistics Applications and Probability, pp. 105-122, 1 6 2017.
[31] N. S. Khalaf, A. Hameed, K. Moudher , M. A. Khaleel and Z. M. Abdullah, "the Topp Leone flexible Weibull distribution: an extension of the flexible Weibull distribution," International Journal of Nonlinear Analysis and Applications, pp. 2999-3010, 1 13 2022.
[32] A. Khaoula, N. Seddik-Ameur, A. A. Abd El-Baset and M. A. Khaleel, "The Topp-Leone Extended Exponential Distribution: Estimation Methods and Applications," Pakistan Journal of Statistics and Operation Research, pp. 817-836, 4 18 2022.
[33] H. Sharqa , M. Ahsan-ul-Haq, J. Zafar and M. A. Khaleel, "Unit Xgamma Distribution: Its Properties, Estimation and Application: Unit-Xgamma Distribution," Proceedings of the Pakistan Academy of Sciences: A. Physical and Computational Sciences, pp. 15-28, 1 59 2022.
[34] G. P. Dhungana and V. Kumar, "Exponentiated Odd Lomax Exponential distribution with application to COVID-19 death cases of Nepal," PloS one, p. e0269450, 6 17 2022.
Downloads
Published
Issue
Section
License
Copyright (c) 2025 Kamal Najim Abdullah, Nooruldeen Alsaab Noori , Mundher A. khaleel (Author)

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Licensed under a CC-BY license: https://creativecommons.org/licenses/by-nc-sa/4.0/







