On the Theory and Pliability of Regressogram Decomposition: Application and Simulation Sensitivity of the Olanrewaju-Olanrewaju Kernel-Based Regressogram
DOI:
https://doi.org/10.62933/7tz4w241Keywords:
Bandwidth, Generalized Cross-Validation, Kernels, Nadaraya-Watson Kernel-Estimator , RegressogramAbstract
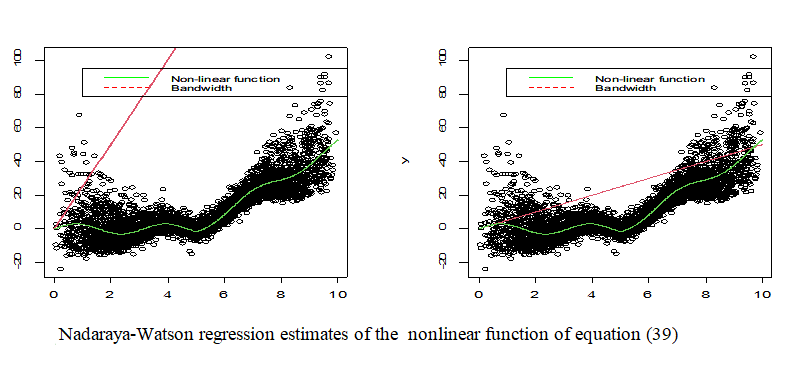
This paper studies the pliability of regressogram decomposition as a technique of modeling bivariate random measurements of (X_1,Y_1),…,(X_n,Y_n) either via equal-width bins or linear smoother with the use of nonparametric, Olanrewaju-Olanrewaju, and machine-learning Boxcar kernels. The nonparametric, Olanrewaju-Olanrewaju, and Boxcar kernels were differently incorporated into the Nadaraya-Watson kernel-estimator as a generalized Mercer kernel. The optimal bandwidth needed as a smoothing parameter for impelling the kernel-based regressogram was derived with the aid of Generalized Cross-Validation (GCV). Finite and countable sample size bound required for the regressogram modeling was ascertained for reasonable sample sizes needed for effective optimization of coefficients, and deductive measurable of some error indexes via strongly universally consistent estimator. In conclusion, the Olanrewaju-Olanrewaju kernel-based regressogram was notably sensitive with the smallest magnitude of scale estimated (σ^2) and GCV estimates in application to real life dataset and simulation study to the nonparametric Doppler regression function.
References
[1] M. Mächler, “Nonparametric regression,” Seminar Für Statistik, ETH Zürich, Switzerland, 2018, pp. 1-35.
[2] Berrett, T. B. (2021). Strongly universal consistent nonparametric regression and classification with privatized data. Electronic on Statistics, 18(15), 2430-2453.
[3] Hofymer, D. P. (2021). Fast exact evaluation of univariate kernel sums. IEEE Transactions on Pattern Analysis and Machine Intelligence, 43, 447-458.
[4] Correa, J. P., Kneib, T., Ospina, R., Tejada, J., and Marmolejo-Ramos, F. (2020). Assessing the potential heteroscedasticity in psychological data: A GAMLSS approach deep learning approach. The Quantitative Methods for Psychology, 19(4), 333-346.
[5] Farokhi, F. (2025). Deconvoluting kernel density estimation and regression for locally differentially private data. Scientific Report, 10(1), 8-30.
[6] Hofymer, D. P. (2022). Fast kernel smoothing in R with applications to projection pursuit. Journal of Statistical Software, 101(3), 1-33.
[7] T. Hastie, R. Tibshirani, and J. Friedman, “Elements of statistical learning:data mining inference and prediction. Springer, Second Edition, 2009.
[8] L. Györfi, M. Kohler, A. Krzyzak, and H.A. Walk, “A Distribution-free theory of nonparametric regression. Springer, 2002.
[9] A. Bowman, and A. Azzalini, “ Sm: Smoothing methods of nonparametric regression and density estimation. R Package version 2.2-5.7, 2021.
[10] Langrené, N., & Warin, X. Fast and stable multivariate kernel density estimation by fast sum updating. Journal of Computational Graphical Statistics, 28(3), 596-608.
[11] Yen-Chin, C. “STAT 415 introduction to nonparametric statistics, lecture 9: regression: regressogram and kernel regression, winter, 2018.
[12] Li, Q, Lin, J., & Racine, J. S. (2013). Optimal bandwidth selection for nonparametric distribution and quantile functions. Journal of Business and Economic Statistics, 31, 57-65.
[13] Noh, H. (2014). Estimation using kernel smoothing with data transformation. Journal of the Korean Statistical Society, 43, 503-514.
[14] Li, Q., Maasounmi, E., & Racine, J.S. (2009).A nonparametric test for equality of distributions with mixed categorical and continuous data. Journal of Econometrics, 148,186-200.
[15] Sparapani, R., Spanbauer, C., & McCulloch,R. (2021). Nonparametric machine learning and efficient computation with Bayesian additive regression trees: The BART R Package. Journal of Statistical Software, 97(1), 457-472.
[16] Erillis, N.A., & Alakus, K. (2014). Non-parametric regression estimation for data with equal values. European Scientific Journal, 10(4), 72-82.
[17] Walker, J., Poliziani, C., Tortora, C., Schweizer, J., & Rupi, F. (2022). Nonparametric regression analysis of cyclist waiting times across three behavioural typologies. ISPRS International Journal of Geo-information, 11(3), 3-14.
[18] Tsagris, M. Alenazi, A., & Stewart, C. (2023). Flexible non-parametric regression models for compositional response data with zeros. Statistics and Computing, 33(106), 1-17.
[19] B. E. Hansen. Lecture notes on nonparametrics. University of Wisconsin, Spring, 2009.
[20] J. Fox, and S. Weisberg, An R companion to applied regression. Sage, Thousand Oaks, CA, Third Edition, 2019.
[21] R. Tibshirani, and L. Wasserman, “Nonparametric regression: statistical machine learning,” Spring, 2012.
[22] J.W. Tukey, “Curves as parameters and toch estimation,” Proc. 4th Berkeley Symposium, 681-694, 1961.
[23] Tukey, J.W. (1947). Nonparametric estimation II. statistically equivalent blocks and tolerance Regions. The continuous case, Annals of Mathematical Statistics, 18, 529-539.
[24] Olanrewaju, R.O. (2020). Penalized likelihood estimation of gamma distributed response variable via corrected solution of regression coefficients. Journal of Modern Applied Statistical Methods, 19(1), 1-18.
[25] Olanrewaju, R.O., & Olanrewaju S. A. (2024). On the Efficiency of the newly proposed Olanrewaju- Olanrewaju (L_((O-O)λ_(γ(|θ|)) )) penalized regression-type estimator via GLMs technique. Studies of Applied Economics, 42(1), 1-23.
[26] L. Györfi, M. Kohler A. Krzyzak, and H.A. Walk “Distribution-free theory of nonparametric regression,” Springer Science and Business Media, 2006.
Downloads
Published
Issue
Section
License
Copyright (c) 2025 Rasaki Olawale Olanrewaju , Sodiq Adejare Olanrewaju (Author)

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Licensed under a CC-BY license: https://creativecommons.org/licenses/by-nc-sa/4.0/







