Bayesian Prediction of a Hybrid Spatial Model When It Follows a Multivariate Cauchy Distribution

Abstract

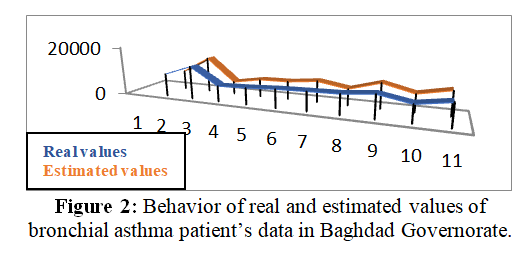
Spatial models are important economic models that deal with the spatial dimensions of the data of the phenomenon under study. These models have several forms, including the spatial autoregressive model, spatial error, spatial Durbin, and others. In this research, two spatial models were hybridized, namely the spatial autoregressive model and spatial error, and the parameters of the hybrid spatial model were estimated using the Bayesian method when the initial distribution of the parameter to be estimated belongs to the family of known probability distributions when the error of the hybrid spatial model follows a multivariate Cauchy distribution, in addition to finding the predictive distribution of the hybrid model. The researchers concluded that the predictive distribution of the vector of future observations of the hybrid spatial model is an uncommon but appropriate probability distribution (Proper). Through the properties of mathematical expectation, the Bayesian prediction was found. The application was applied to real data related to the number of people with bronchial asthma in Baghdad Governorate for the year (2004). If the number of people with bronchial asthma was studied as a response variable and the variables of lead, carbon monoxide, sulfur dioxide and total suspended particles as variables affecting bronchial asthma, the researchers concluded, based on the (MatlabR2022a) program, that the estimated hybrid spatial model outperformed the estimated general regression model and that the Bayesian method was suitable for conducting the process of predicting future observations, in addition to the fact that the variables of carbon monoxide, sulfur dioxide and total suspended particles have significant effects on the incidence of bronchial asthma