On Inference of Finite Mixture of Rayleigh Distribution by Gibbs Sampler and Metropolis-Hastings
DOI:
https://doi.org/10.62933/93v3c985Keywords:
Mixture of Rayleigh Distribution , Bayesian inference, Gibbs Sampler, Metropolis- Hastings, Bayesian Information Criteria(BIC)Abstract
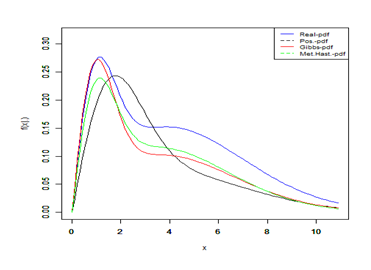
Inferential methods of statistical distributions have reached a high level of interest in recent years. However, in real life, data can follow more than one distribution, and then mixture models must be fitted to such data. One of which is a finite mixture of Rayleigh distribution that is widely used in modelling lifetime data in many fields, such as medicine, agriculture and engineering. In this paper, we proposed a new Bayesian frameworks by assuming conjugate priors for the square of the component parameters. We used this prior distribution in the classical Bayesian, Metropolis-hasting (MH) and Gibbs sampler methods. The performance of these techniques were assessed by conducting data which was generated from two and three-component mixture of the Rayleigh distribution according to several scenarios and comparing the results of the scenarios by calculating the mean of classification successful rate (MCSR) and the mean of mean square error(MMSE). The results showed that Gibbs sampler algorithm yields a better computation results than the others in terms of MMSE and MCSR.
References
Jones, P. N., & McLachlan, G. J. (1990). Laplace-normal mixtures fitted to wind shear data. Journal of Applied Statistics, 17(2), 271–276.
Kanji, G. K. (1985). A mixture model for wind shear data. Journal of Applied Statistics, 12(1), 49–58.
Harris, C. M. (1983). On finite mixtures of geometric and negative binomial distributions. Communications in Statistics-Theory and Methods, 12(9), 987–1007.
Rao, G. S. (2012). Estimation of reliability in multicomponent stress-strength based on generalized exponential distribution. Revista Colombiana de Estadistica, 35(1), 67–76.
Ueda, N., Nakano, R., Ghahramani, Z., & Hinton, G. E. (2000). SMEM algorithm for mixture models. Neural Computation, 35(1), 2109–2128.
Peel, D., & McLachlan, G. J. (2000). Robust mixture modelling using the t distribution. Statistics and Computing, 10, 335–344.
Cadez, I. V., McLaren, C. E., Smyth, P., & McLachlan, G. J. (1999). Hierarchical models for screening of iron deficiency anemia. In Proceedings of the Sixteenth International Conference on Machine Learning (pp. 77–86). Morgan Kaufmann.
Lehmann, E. L. (1980). Efficient likelihood estimators. The American Statistician, 34, 233–235.
Lehmann, E. L. (1983). Theory of Point Estimation. Wiley.
Montuelle, L., & Le Pennec, E. (2014). Mixture of Gaussian regressions model with logistic weights, a penalized maximum likelihood approach. Electronic Journal of Statistics, 8(1), 1661–1695.
Boldea, O., & Magnus, J. R. (2009). Maximum likelihood estimation of the multivariate normal mixture model. Journal of the American Statistical Association, 104(488), 1539–1549.
Karlis, D., & Xekalaki, E. (1999). On testing for the number of components in finite Poisson mixtures. Annals of the Institute of Statistical Mathematics, 51(1), 149–162.
Henna, J. (1985). On estimating the number of constituents of a finite mixture of continuous distributions. Annals of the Institute of Statistical Mathematics, 37, 235–240.
Liu, C., & Rubin, D. B. (1998). Maximum likelihood estimation of factor analysis using the ECME algorithm with complete and incomplete data. Statistica Sinica, 8, 729–747.
Louis, T. A. (1982). Finding the observed information matrix when using the EM algorithm. Journal of the Royal Statistical Society: Series B (Methodological), 44(2), 226–233.
Liu, C., & Rubin, D. B. (1995). ML estimation of the t distribution using EM and its extensions, ECM and ECME. Statistica Sinica, 5(1), 19–39.
Ali, F., & Zhang, J. (2017). Mixture model-based association analysis with case-control data in genome wide association studies. Statistical Applications in Genetics and Molecular Biology, 16(3), 173–187.
Mohammed, N., & Ali, F. (2022). Estimation of parameters of finite mixture of Rayleigh distribution by the expectation-maximization algorithm. Journal of Mathematics, 2022(1), 1–7.
Ali, F. (2023). Bayesian methods for estimation of parameters of finite mixture of inverse Rayleigh distribution. Mathematical Problems in Engineering, 2023, 1–9.
Wong, C. S., & Li, W. K. (2000). On a mixture autoregressive model. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 62(1), 95–115. https://doi.org/[DOI]
Le, N. D., Martin, R. D., & Raftery, A. E. (1996). Modeling flat stretches, bursts, and outliers in time series using mixture transition distribution models. Journal of the American Statistical Association, 91(436), 1504–1514. https://doi.org/[DOI]
Tanner, M. A., & Wong, W. H. (1987). The calculation of posterior distributions by data augmentation (with discussion). Journal of the American Statistical Association, 82(398), 528–550.
Gelfand, A. E., & Smith, A. F. M. (1990). Sampling-based approaches to calculating marginal densities. Journal of the American Statistical Association, 85(410), 398–409.
Cowles, M. K., & Carlin, B. P. (1996). Markov chain Monte Carlo convergence diagnostics: A comparative review. Journal of the American Statistical Association, 91(434), 883–904.
Celeux, G., Hurn, M., & Robert, C. P. (2000). Computational and inferential difficulties with mixture posterior distributions. Journal of the American Statistical Association, 95(451), 957–970.
Brooks, S. P. (2001). On Bayesian analysis and finite mixtures for proportions. Statistics and Computing, 11(3), 179–190.
Viallefont, V., Richardson, S., & Green, P. J. (2002). Bayesian analysis of Poisson mixtures. Journal of Nonparametric Statistics, 14(1-2), 181–202.
Pezoulas, V. C., Tachos, N. S., Gkois, G., Olivotto, I., Barlocco, F., & Fotiadis, D. I. (2022). Bayesian inference-based Gaussian mixture models with optimal components estimation towards large-scale synthetic data generation for in silico clinical trials. IEEE Open Journal of Engineering in Medicine and Biology, 3, 108–114.
Simola, U., Cisewski-Kehe, J., & Wolpert, R. L. (2021). Approximate Bayesian computation for finite mixture models. Journal of Statistical Computation and Simulation, 91(6), 1155–1174.
Su, X., Zamzami, N., & Bouguila, N. (2022). A fully Bayesian inference with Gibbs sampling for finite and infinite discrete exponential mixture models. Applied Artificial Intelligence, 36(1).
Hartigan, J. A., & Wong, M. A. (1979). A k-means clustering algorithm. Applied Statistics, 28(1), 100–108.
Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., & Rubin, D. B. (2013). Bayesian Data Analysis (3rd ed.). CRC Press.
Downloads
Published
Issue
Section
License
Copyright (c) 2024 Fadhaa Ali (Author)

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Licensed under a CC-BY license: https://creativecommons.org/licenses/by-nc-sa/4.0/







