Deep Functional Median Polish: A Robust Framework Integrating Functional Depth and Median-Based Decomposition for Long-Term Financial Time Series
DOI:
https://doi.org/10.62933/vm6bdz11Keywords:
Functional Data Analysis, Functional Median Polish, Deep Functional Median Polish, Financial Time Series, Seasonal Decomposition, Robust Functional ModelingAbstract
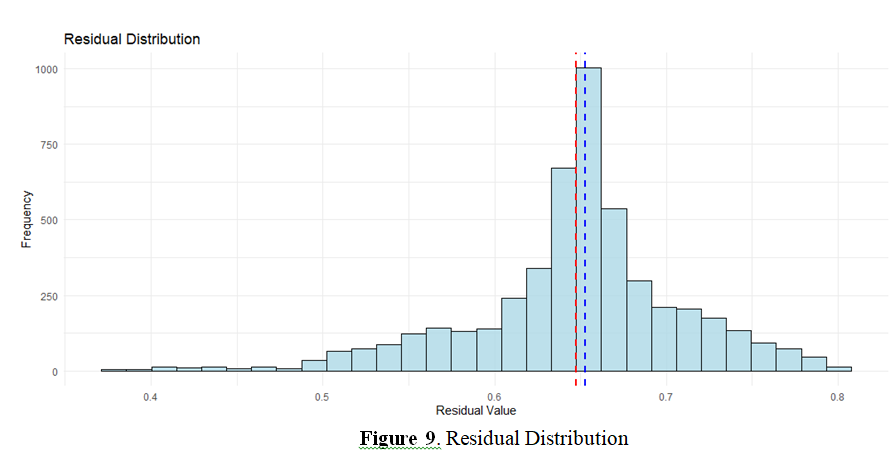
This research builds upon the successive development of robust functional analysis methods, starting with the Median Polish (MP) algorithm, which provided a powerful additional model for handling bidirectional data, progressing through Functional Median Polish (FMP), and culminating in the integration of functional depth measures into a single framework. This work presents a new framework called Deep Functional Median Polish (Deep FMP), which combines the robustness of median statistics in the MP algorithm with the inherent geometric properties of functional depth measures to characterize the hierarchical structure of complex functional time series. Also applies the proposed model to financial data spanning 34 years, comprising 408 views structured in a 34×12 matrix. Each year is transformed into a smoothed function using Fourier's rule, and then PCA is used to derive a highly interpreted latent space, where the first component explains 94.3% of the total variance. Subsequently, the median model is applied to the latent space to separate the general, annual, seasonal, and residual components. The results demonstrated a high capacity for accurately reconstructing time-related behaviour, with near-normal residuals centred around 0.65, and a clear seasonal distribution that increases in January and December and decreases in the middle of the year.
The results prove that combining depth measures with Median Polish provides high explanatory power and enhances the model's resistance to outliers, with clear applicability to economic data with complex time-related patterns. This model opens the way for future applications in forecasting, risk analysis, and detecting structural shifts in long-term functional data.
References
[1] Ajoge, I. (2017). Median polish techniques for analysing paired data ( Doctoral dissertation, master thesis, Putra Malaysia).
[2] Berke, O. (2001). Modified median polish kriging and its application to the Wolfcamp–Aquifer data. Environmetri cs: The official journal of the International Environmetrics Society, 12(8), 731–748.
[3] Dammer, E. B., Seyfried, N. T., & Johnson, E. C. (2023). Batch correction and harmonization of –Omics datasets with a tunable median polish of ratio. Frontiers in Systems Biology, 3, 1092341.
[4] Elías, A., & Nagy, S. (2025). Statistical properties of partially observed integrated functional depths. TEST, 34(1), 125–150.
[5] Huang, H., & Sun, Y. (2016). Total variation depth for functional data. arXiv preprint arXiv:1611.04913.
[6] Husain, Q. N., Adam, M. B., Shitan, M., & Fitrianto, A. (2016). Extension of Tukey’s smoothing techniques. Indian Journal of Science and Technology, 9(28), 1–5.
[7] Jayaram, B., & Klawonn, F. (2012). Generalised median polish based on additive generators. In Synergies of Soft Computing and Statistics for Intelligent Data Analysis (pp. 439–448). Berlin, Heidelberg: Springer.
[8] Jiménez Varón, C. F. (2024). Visualization, characterization, and forecasting of multivariate and functional time series.
[9] Klawonn, F., Jayaram, B., Crull, K., Kukita, A., & Pessler, F. (2013). Analysis of contingency tables based on generalised median polish with power transformations and non-additive models. Health Information Science and Systems, 1(1), 11.
[10] López-Pintado, S., & Romo, J. (2009). On the concept of depth for functional data. Journal of the American Statistical Association, 104(486), 718–734.
[11] Luo, M., Nagy, S., Ogden, T., & López-Pintado, S. (2025). The quantile integrated depth with applications to noisy functional data. Journal of Computational and Graphical Statistics, 1–20.
[12] Martínez-Hernández, I., Genton, M. G., & González-Farías, G. (2019). Robust depth-based estimation of the functional autoregressive model. Computational Statistics & Data Analysis, 131, 66–79.
[13] Qu, Z., Dai, W., & Genton, M. G. (2021). Robust functional multivariate analysis of variance with environmental applications. Environmetrics, 32(1), e2641.
[14] Rigueira, X., Olivieri, D., Araujo, M., Saavedra, A., & Pazo, M. (2025). Multivariate functional data analysis and machine learning methods for anomaly detection in water quality sensor data. Environmental Modelling & Software, 190, 106443.
[15] Sguera, C., Galeano, P., & Lillo, R. E. (2016). Functional outlier detection by a local depth with application to NOx levels. Stochastic Environmental Research and Risk Assessment, 30(4), 1115–1130.
[16] Sun, Y., & Genton, M. G. (2012). Functional median polish. Journal of Agricultural, Biological, and Environmental Statistics, 17(3), 354–376.
[17] Tukey, J. W. (1977). Exploratory data analysis. Reading, MA: Addison-Wesley.
[18] Zuo, Y. (2003). Projection-based depth functions and associated medians. The Annals of Statistics, 31(5), 1460–1490.
Published
Issue
Section
License
Copyright (c) 2026 Abdulsalam M. Sabri (Author)

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Licensed under a CC-BY license: https://creativecommons.org/licenses/by-nc-sa/4.0/







