Bayesian method estimation for Exponential and Weibull Survival regression models

Abstract

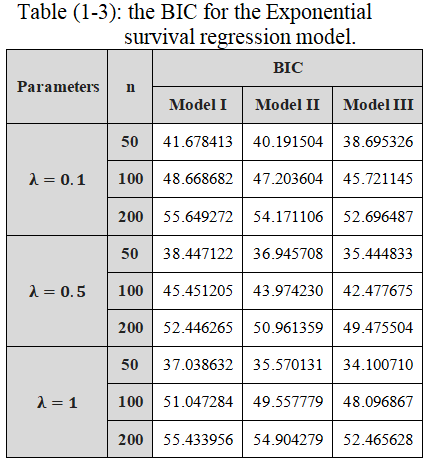
Parametric regression models are one of the most important regression models used in the medical field. They are the tool through which the response variable is modeled when the values ​​of that variable are survival times with a known probability distribution such as the exponential distribution and the Weibull distribution, I propose in this article to estimate the parameters of parametric survival regression models using the Bayesian method, these models are: the exponential survival regression model, the Weibull survival regression model, The simulation was used to generate data that follows the parametric survival regression models depending on various factors such as sample size, and three different parameter models, The simulation results showed that the exponential survival regression model outperformed the Weibull survival regression model in order to obtain the lowest value according to the Bayesian Information Criterion (BIC), The larger the sample size, the more accurate and reliable the analysis estimators performed by the Bayes Information Criterion.