Estimation of Transition Probabilities in Multi-State Survival Data
DOI:
https://doi.org/10.62933/swsd0n89Keywords:
Survival Data;, Multi – Marcov State model;, Nelson-Aalen Estimator;, Aalen-Johansen Estimator;, Kaplan-Maeier Estimator;, Multi-State Model;, Hazard Function.Abstract
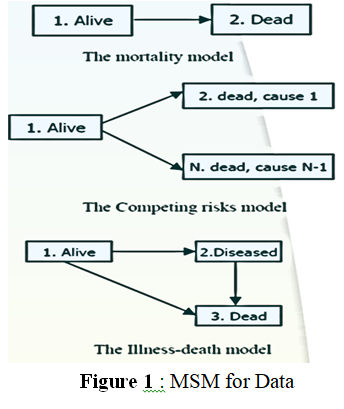
This study calculates nonparametric estimators including Kaplan-Meier, Nelson-Aalen and Aalen - Johnson for applying the Multi-State Model (MSM ) to analyze type IIIness-death transitions between alive and death followed by different duct cancer types (Breast, Lung , Brain , Ovary) through reduction techniques by using diminutions (k+1)*(k+1) for matrix , The package software program was used to generate elementary Nelson-Aalen and Kaplan-Meier estimator.
References
[1] Aalen, O. (1978). Nonparametric estimation of partial transition probabilities in multiple decrement models. The Annals of Statistics, 6(3), 534-545.
[2] Aalen, O. & Johansen, S. (1978). An empirical transition matrix for non-homogeneous Markov chains based on censored observations. Scandinavian Journal of Statistics, 141-150.
[3] Andersen.P.K,Borgan Gill R. D. and Keiding (1993)“ Statistical Models Based on Counting Processes” Springer Verlag, New York.
[4] Balboa, V., & De Uña Alvarez, J. (2018). Estimation of transition probabilities for the illness-death model: Package tp. idm. Journal of Statistical Software. Biometrics,34,571-580.
[5] Borgan, Ø. (1997). Three Contributions to the Encyclopedia of Biostatistics: The Nelson-Aalen, Kaplan-Meier, and Aaalen-Johansen Estimators. Department of Mathematics, University of Oslo.
[6] Fleming, T. R. (1978a). Nonparametric estimation for nonhomogeneous Markov processes in the problem of competing risks. The Annals of Statistics, 1057-1070.
[7] Fleming, T. R. (1978b). Asymptotic distribution results in competing risks estimation. The Annals of Statistics, 1071-1079.
[8] Fleming.T.R.and Harrington. D. P.(1991) “Counting Processes and Survival Analysis”,Wiley ,New York.
[9] Heggland, T. (2015). Estimating transition probabilities for the illness-death model (Master's thesis).
[10] Hornung . R. and Meinhardt .T (1987) “Quantitative risk assessment of lung cancer” in (US) uranium Miners Health Physics,52,417-30.
[11] Johansen. S. (1978) “The product limit estimator as maximum likelihood estimator” Scandinavian Journal of Statistics,5,195-199.
[12] Kalbfeisch,J.D.and Prentice. R. L.(1980) “The Statistical Analysis of Failure Time Data “,Wiley,New York.
[13] Kaplan. E. L. and Meier.P (1958) “Non_parametric estimation from incomplete observations” Journal of the American Statistical Associatio.53,451-481.
[14]Keiding.N.and Andersen.P.K. (1989) ”Nonparametric estimation of transition intensities and transition probabilities a case study of a two state Markov process” ,Applied Statistics,38.
[15] Llopis-Cardona, F., Armero, C., & Sanfélix-Gimeno, G. (2021). Reflection on modern methods: competing risks versus multi-state models. arXiv preprint arXiv:2104.03671.
[16] Ma, Y. (2022). Nonparametric Estimation of Transition Probabilities in Illness-Death Model Based on Ranked Set Sampling (Doctoral dissertation, University of South Florida).
[17] Machado, L. F. M., & Roca-Pardiñas, J. (2011). p3state. msm: Analyzing survival data from an illness-death model. Journal of Statistical Software, 38, 1-18.
[18] Maltzahn, N., Hoff, R., Aalen, O. O., Mehlum, I. S., Putter, H., & Gran, J. M. (2021). A hybrid landmark Aalen-Johansen estimator for transition probabilities in partially non-Markov multi-state models. Lifetime Data Analysis, 27, 737-760.
[19] Manevski, D., Putter, H., Pohar Perme, M., Bonneville, E. F., Schetelig, J., & de Wreede, L. C. (2022). Integrating relative survival in multi-state models—a non-parametric approach. Statistical Methods in Medical Research, 31(6), 997-1012.
[20] Nair.V. N (1984) “Confidence bands for survival functions with censored data,A comparativestudyTechnometrics”,26,265-275.
[21] Nelson, W. (1972). Theory and applications of hazard plotting for censored failure data. Technometrics, 14(4), 945-966.
[22] Nelson. W. (1969)“Hazard plotting for incomplete failure data” Journal of Quality Technology,1,27-52.
[23] Nießl, A., Allignol, A., Beyersmann, J., & Mueller, C. (2023). Statistical inference for state occupation and transition probabilities in non-Markov multi-state models subject to both random left-truncation and right-censoring. Econometrics and Statistics.
[24] Nyinawajambo, M. R. (2018). Survival Analysis of Time to Event Data: An application to child mortality in Sub-Saharan Africa Region using Their Demographic and Health Surveys.
[25]Schliching.P.Christensen.E.Andersen.P.K.Fauerholdt.L.Juhl.E.Poulsen.H.and Tygstrup .N (1983)”for The Copenhagen Study Group for Liver Diseases Prognostic factors in cirrhosis identied by Cox;s regression model “ Hepatology ,3,889-893.
[26] Snijders, M. (2017). Prediction for Transition Probabilities in Multi-State Models (Bachelor's thesis).
[27] Soutinho, G. U& Meira-Machado, L. U (2020). Estimation of the transition probabilities in multi-state survival data: New developments and practical recommendations. WSEAS Transac Math. 2020; 19: 353-366.
[28] Temkin, N. R. (1978). An analysis for transient states with application to tumor shrinkage. Biometrics, 571-580.
Downloads
Published
Issue
Section
License
Copyright (c) 2025 Haider kareem Raheem , Hayder yahya mohammed (Author)

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Licensed under a CC-BY license: https://creativecommons.org/licenses/by-nc-sa/4.0/







